The Rubens tube I made a while back puts on a fairly impressive show when its speaker is driven with music or a noise box, as was done during the Milwaukee Makerspace Grand Opening.  The story is somewhat different when it is used to display the acoustic standing wave pattern inside the tube.  When a single tone (sine wave) at a resonance frequency of the system is played though the speaker, the heights of the flames map out the sinusoidal shape along the length of the tube. There are two very important variables whose values determine how well this will work.  These are the acoustic pressure in the tube, which is set by the speaker and its input voltage, and the propane gas pressure, which is set by a regulator or the valve on the propane bottle.  Even a professionally made Rubens tube has a relatively small range of these two pressure settings that create a nice sine wave distribution of flame heights.

After running my Rubens tube for a short while, I realized I’d made a few design choices that make the already small range of good operating parameters even smaller.  First, I didn’t actually use a gas regulator, I only used the valve on the propane nozzle.  Note that the propane flow rate is highly affected by the temperature of the nozzle, so the propane tank must be kept in a water-filled bucket to prevent the outlet valve from freezing up.  Just like a gas pressure regulator can be used, so could an acoustic pressure regulator (i.e. a compressor).  This could help prevent the flames from extinguishing during particularly dynamic musical passages.  Alternately, some type of pilot light system could be devised so that the flames automatically relight – perhaps glowing red nichrome wire could be added in a moderately safe way.  I also spaced the fifty 0.043” diameter holes apart by only 0.9 inches.  Having this many holes reduces the amplitude of the resonances, making them more difficult to ‘find’ by simply listening to the amplitude when adjusting the frequency input to the speaker.   Better performance would be achieved by having fewer holes spaced further apart.  Lastly, I’ve used a pipe whose inner diameter is only 2.5 inches.  A larger diameter pipe would further increase the amplitude of the resonances.

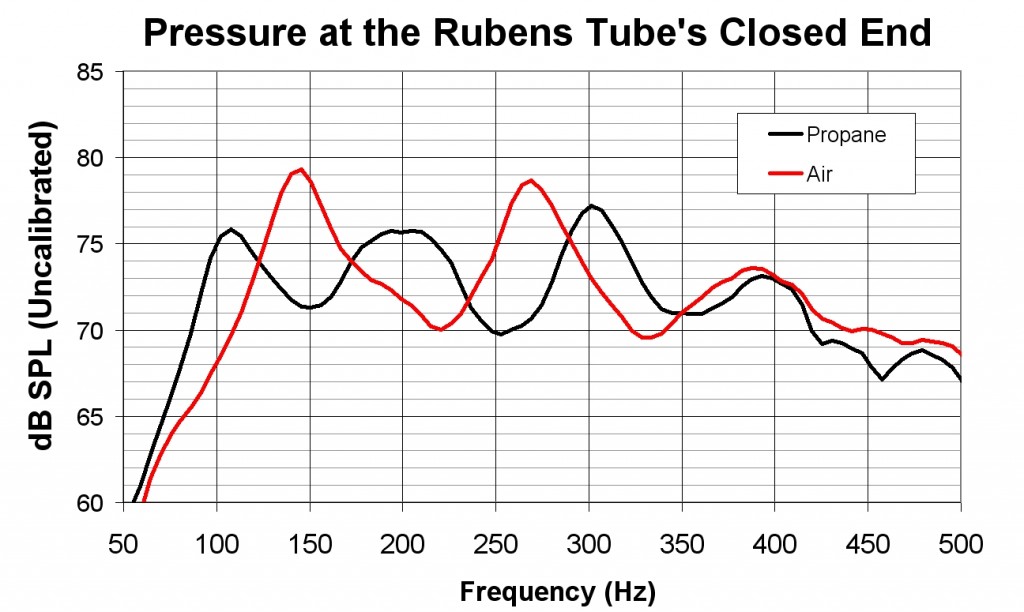
I put an electret microphone inside the Rubens tube at the end opposite the speaker, and measured the pressure inside while electrically driving the speaker with pink noise.  I did this with both air and propane inside the tube.  The following graph shows the low amplitude of the tube’s resonances with propane inside — between 4 and 7 dB.

The other interesting bit of data one can find from this graph is the speed of sound in propane.  Knowing the sound speed, one can calculate either the length of pipe needed to have a particular fundamental resonance frequency (n=1) or if a particular speaker has a resonance frequency low enough to excite the fundamental resonance of a particular length Rubens tube.  The resonance frequencies of a tube having uniform cross sectional area and two rigidly closed ends are given by: Fn = nC/(2*L), where n is the nth mode, C is the sound speed, and L is the length of tube.  The Rubens tube doesn’t have two closed ends, it has a paper cone speaker at one end.  It also doesn’t have uniform area – it has a small open volume in front of the speaker.  Both of these will change the “effective” length of the tube.  Don’t worry though, we can use the measured resonance frequencies with air in the tube to calculate the effective length: Leff = nC/(2*Fn).  Knowing C=343 m/s in air, we can use the measured resonances of the first three modes  (144 Hz, 262 Hz and 380 Hz) to find that the (averaged) effective length is 1.28m.  Using this effective length and the lowest three resonance frequencies (108 Hz, 205 Hz, and 300 Hz) with propane in the tube, Fn = nC/(2*Leff) predicts the sound speed to be ~265 m/s.

Makerspace members or any other folks near Milwaukee should feel free to stop by (on Tuesdays or Thursdays evenings) and fire up the Rubens tube.  Just use a small amplifier so you don’t put more than 30 Watts into the 4” speaker!  For some scholarly information about Rubens tubes, check  out the series of articles in the journal “The Physics Teacher:”  M. Iona (14), p325 from 1976; T. Rossing (15), P260 from 1977; R Bauman (15) p448 from 1977; and G. Flicken (17) p306 from 1979.